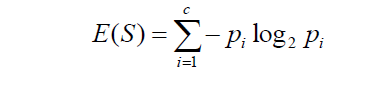Apa Itu Entropy dan Information Gain ? Bagaimana Menghitungnya ?

Entropy singkatnya adalah satuan untuk mengukur ketidak pastian
Pertama kita perlu mengetahui cara menghitung entropy

Nilai entropy berkisar antara  0 sampai 1 , Jika bernilai 0 berarti ketdak pastian sangat rendah  sedangkan saat nilainya 1  berarti ketidak pastian sangat tinggi
, contoh keadaan ketidak pastian tinggi adalah saat kalian disuruh memprediksi bola merah atau bola biru yang akan muncul dari kotak , padahal di dalam kotak ada 5 bola merah dan 5 bola biru. Maka ketidak pastiannya sangat tinggi / maksimal. Sedangkan jika di dalam kotak ada 10 bola merah dan 0 bola biru maka ketidak pastian nya sangat rendah dengan kata lain bola yang akan muncul PASTI bola merah.

Anggap saja simbol  ( - ) adalah bola biru dan simbol (+) adalah bola merah, maka beginilah perubahan entropy nya








Lalau bagaimana menghitung Information Gain
Information gain adalah kemampuan suatu feature untuk mengurangi ketidak pastian dalam melakukan klasifikasi

Information gain biasa dipakai untuk feature selection dalam klasifikasi

caranya adalah dengan menghitung entropy (ketidak pastian) dari target yang akan diprediksi tanpa diberi informasi feature apapaun. Lalu hasil dari penghitungan  dikurangi entropy dari target yang akan akan diprediksi TAPI dengan diberi informasi yaitu satu feature

untuk lebih jelasnya kita lihat ini

Kalau kalian mencari kodenya, maka kodenya sebagai berikut

import math
import numpy as np
def calculate_IG(X, y):
    def entropy_of_y(y):
        value_to_average =[]
       
        y_unique = np.unique(y)
       
        value_to_sum = []
        for y_unique_i in y_unique:
            event = 0
            outcome = 0
            for y_i in y:
               
              
                if y_i ==y_unique_i:
                    event +=1
               
                outcome += 1
               
                   
            p = event/outcome
           
            value_to_sum.append(-p * math.log(p,2))
       
       
           
       
        return sum(value_to_sum)
           
       
    def entropy_of_yX(X, y):
       
        value_to_average =[]
       
        y_unique = np.unique(y)
        X_unique = np.unique(X)
        for X_unique_i in X_unique:
            print(X_unique_i)
            value_to_sum = []
            for y_unique_i in y_unique:
                event = 0
                outcome = 0
                for X_i , y_i in zip(X.T, y.T):
                   
                    if X_i == X_unique_i and y_i == y_unique_i:
                        event += 1
                       
                    if X_i == X_unique_i:
                        outcome += 1
                   
                       
                p = event/outcome
                print("p" , p)
                if p > 0:
                    value_to_sum.append(-p * math.log(p, 2))
                else:
                    value_to_sum.append(0)
           
            value_to_average.append(sum(value_to_sum))
           
           
        return np.mean(value_to_average)
           
           
    def gain(X, y):
        return entropy_of_y(y) - entropy_of_yX(X,y)
       
    return gain(X,y)
    
       

X = np.array([1,0,1,1])
y = np.array([1, 0, 0, 1])

print(calculate_IG(X,y))